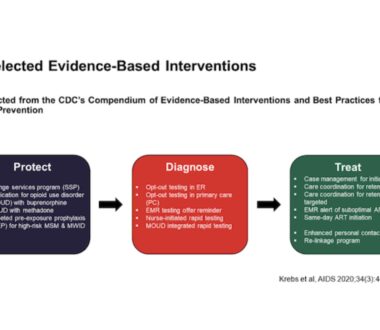
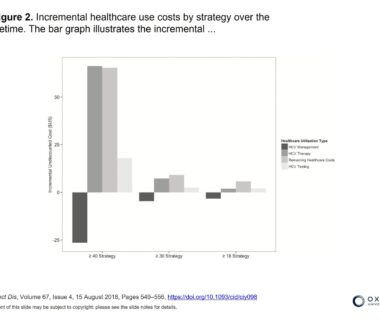
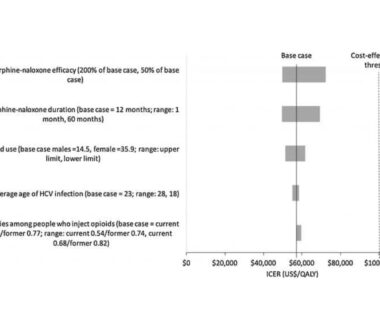
Simulation models integrate up-to-date knowledge about the epidemiology of substance use disorder, treatment outcomes, and resource utilization to make policy-relevant insights about treatment and care. In addition, simulation modeling research allows us to examine benefits and costs from multiple perspectives, such as the community, the healthcare system, the criminal-legal system, or the broader societal perspective. Most importantly, simulation modeling allows us to study scenarios that would not be possible in the real world at the pace required for decision-making.
Methods We Have Used
Markov Modeling
Markov models simulate the progression of a hypothetical cohort of individuals as a series of progressions between “health states.” Using longitudinal data and the medical literature, investigators assign transition probabilities, which govern the movement of a simulated cohort through health states over time. By attaching quality of life weights to each health state, the model generates estimates of quality-adjusted life expectancy. By attaching a cost to each state, the model tabulates the expected lifetime medical costs for the cohort.
Monte Carlo Simulation
Monte Carlo simulation models the progression of a simulated cohort as a series of transitions between health states. Based on longitudinal data and/or the medical literature, the investigator defines probability density functions around key cohort characteristics such as age, sex, and baseline clinical characteristics. The model draws from these distributions to establish each hypothetical person and simulates the clinical course for each person until death. The ability to track individual-level data, as well as the “memory” of clinical or behavioral history, increases the complexity of programming.
Discrete Event Simulation (DES)
DES is programmed to take into account the time between events. The researcher uses data and the medical literature to develop estimates of the rates of each of these events, and from those rates generates a distribution of times to each event. The model then samples from each of the distributions of times to determine which event happens first. The model “fast forwards” through time to that event, and then repeats the process, seeking the time of the next “discrete event.” One advantage of DES is that hypothetical individuals in the model can interact with each other when seeking access to a limited resource allowing for simulation of the delays in obtaining access to care that can occur in real-world settings.
Compartmental Modeling
Compartmental models use differential equations to model the movement of individuals among health conditions. For example, movement from HCV-susceptible to HCV-infected may be modelled as a rate equation as a function of the number of susceptible individuals, the number of infected individuals, an estimate of the frequency with which susceptible and infected individuals share IDU equipment and the probability that a sharing event leads to HCV transmission.
Agent-based Modeling (ABM)
ABM simulates the actions of simulated autonomous agents with the goal of assessing how individual-level interactions impact the system as a whole. ABM defines behaviors for an “agent,” and allows the interactions of such agents to govern movement between health states. Underlying ABM is the concept that simple behavioral rules can generate complex behavior.